関孝和 せきたかかず( A.D.1640〜A.D.1708)
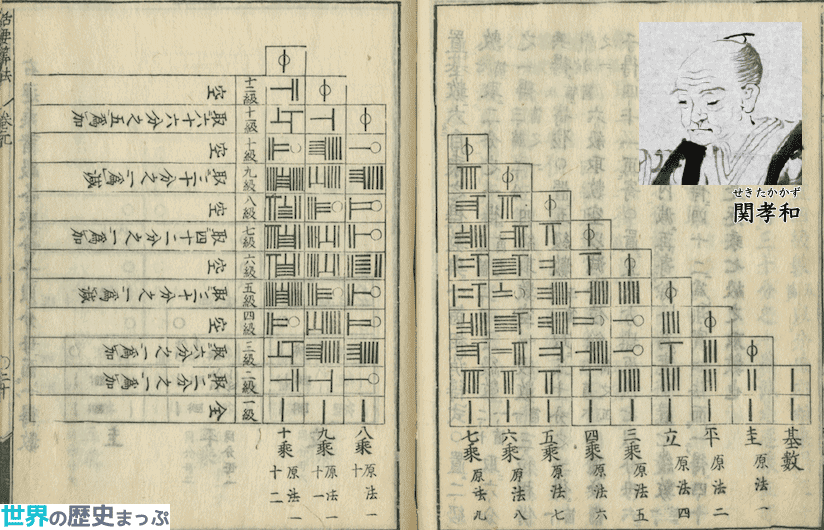
江戸時代初期の和算家。吉田光由の『塵劫記』の内容の段階をさらに高め、縦書きの筆算代数学や微分・積分に類似する方法で、円周率や円の面積などについての解法を示す『発微算法』を著した。
関孝和
江戸時代初期の和算家。通称新助、号は自由亭。甲府藩主徳川綱重(家光の3男)、綱豊(のちの6代将軍家宣)に仕え、綱豊が綱吉の養子となって西の丸に入る(1704)と、孝和も幕府の御納戸組頭となった。和算を、高原吉種に学んだとも、独力で研究したともいわれる。傍書法という方法を編出し、文字係数方程式を扱うことを可能にした(のちに松永良弼が「帰源整法」から「点竄術」に改めた)。中国から伝えられた天元術を発展させて、高次方程式を公式的に解く新しい算法(ホーナーの方法 )を創始した。また行列式の展開法を見出し、正多角形の関係式をつくるのに成功するなど、和算の飛躍に大きく貢献した。弟子に建部賢弘、荒木村英らが知られている。著書に『発微算法』(1674)、『解伏題之法』(83)、『括要算法』(4巻、1712)などがある。
参考 ブリタニカ国際大百科事典
江戸が生んだ大数学者
数学者。上野国の生まれと伝わる。幼児から数学に親しみ、吉田光由の『塵劫記』を独学で理解した。甲府藩から江戸幕府と仕え、西の丸御納戸組頭となる。『発微算法』を著し、筆算による代数計算法を発明して、和算を高等数学に匹敵するレベルに引き上げた。
幕藩体制の展開
元禄文化
諸学問の発達
諸学問の発達(元禄文化)
| 学問 | 人物 | 著作 | 特色 |
|---|---|---|---|
| 本草学 博物学 | 貝原益軒 | 大和本草 | 日本の1362種の動物・鉱物・植物を分類・解説 |
| 養生訓 | 健康法を示す | ||
| 和俗童子訓 | 体系的児童教育書 益軒の著書を元に女性の心得を説く「女大学」もつくられる |
||
| 稲生若水 | 諸物類纂 | 書物の中の物産記事を集大成。加賀藩主前田綱紀が保護 | |
| 農学 | 宮崎安貞 | 農業全書 | 五穀・野菜・果樹の分類とその農業技術の改良・普及 |
| 和算 数学 | 吉田光由 | 塵劫記 | そろばんによるかけ算・わり算の基礎。測量や体積の計算 |
| 関孝和 | 発微算法 | 和算を大成。縦書きの筆算代数式。 円周率や円の面積などについての解法を示す |
|
| 暦学 | 渋川春海 (安井鉢哲) | 貞享暦 | 初代の天文方として平安時代の宣明暦の誤差を修正 |
| 国文学 | 戸田茂睡 | 梨元集 | 和歌に使えない言葉(制の詞)の無意味さと、俗語使用の正当さを説く |
| 契沖 | 万葉代匠記 | 多くの実例と精密な考証で『万葉集』と戸田茂睡の再評価。 徳川光圀の依頼で執筆 |
|
| 北村季吟 | 源氏物語湖月抄 枕草子春曙抄 | 幕府の歌学方として『源氏物語』や『枕草子』の注釈書を書いた |
計算・測量の学として発達してきた和算では、吉田光由(1598〜1672)の著した『塵劫記』の内容の段階をさらに高め、関孝和(1640?〜1708)が筆算代数学や微分・積分に類似する方法で、円の面積を求めるなどの研究を行った。
和算と微積分
世界的な有名人としては、数学者のニュートン(1642〜1727)とライプニッツ(1646〜1716)がイギリスとドイツにいました。これがために関孝和の数学は微積分の創始者と並べられて紹介されることがあったのですが、お互いはもちろん知っていませんでしたし、オランダ経由で微積分が当時の日本に入ってきた形跡は見当たりません。関の数学が微積分のレベルに到達していたということもしばしばいわれますが、幾つかの公式に類似のものがあるものの、全体としてみると当時の和算と微積分は全く発想の異なった数学であり、単純な比較はできません。
参考 江戸の数学
